Improving Local Effectiveness for Global robust training

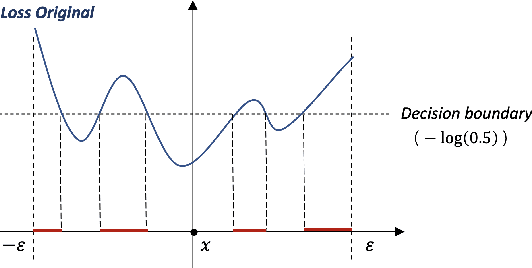
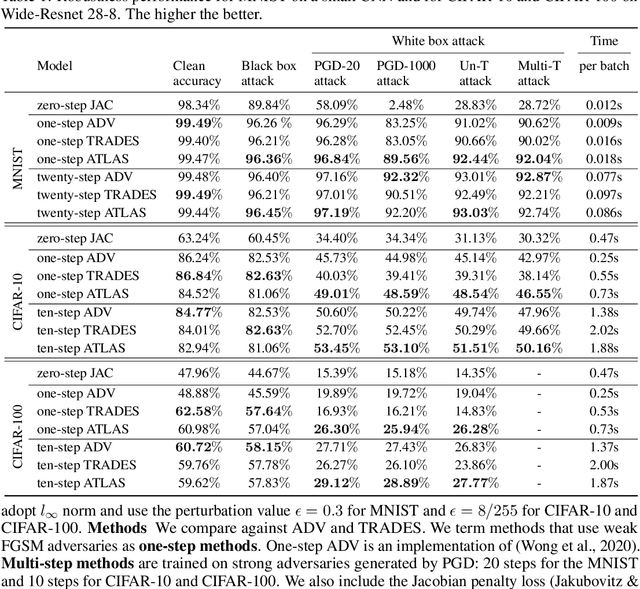
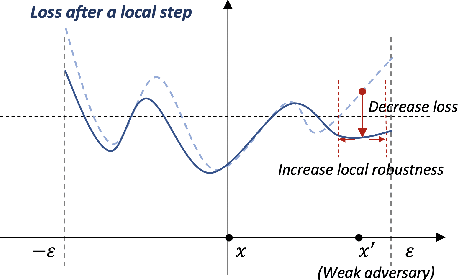
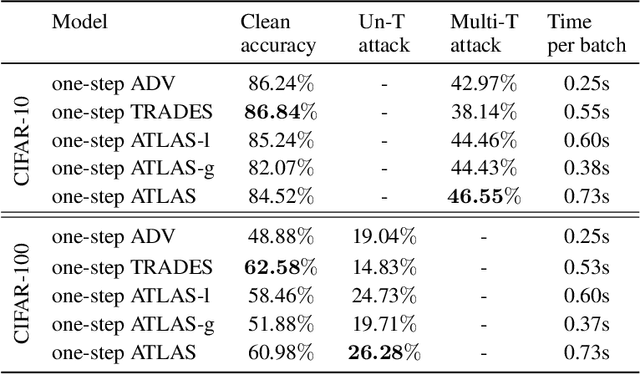
Despite its popularity, deep neural networks are easily fooled. To alleviate this deficiency, researchers are actively developing new training strategies, which encourage models that are robust to small input perturbations. Several successful robust training methods have been proposed. However, many of them rely on strong adversaries, which can be prohibitively expensive to generate when the input dimension is high and the model structure is complicated. We adopt a new perspective on robustness and propose a novel training algorithm that allows a more effective use of adversaries. Our method improves the model robustness at each local ball centered around an adversary and then, by combining these local balls through a global term, achieves overall robustness. We demonstrate that, by maximizing the use of adversaries via focusing on local balls, we achieve high robust accuracy with weak adversaries. Specifically, our method reaches a similar robust accuracy level to the state of the art approaches trained on strong adversaries on MNIST, CIFAR-10 and CIFAR-100. As a result, the overall training time is reduced. Furthermore, when trained with strong adversaries, our method matches with the current state of the art on MNIST and outperforms them on CIFAR-10 and CIFAR-100.

Neural Network Branch-and-Bound for Neural Network Verification

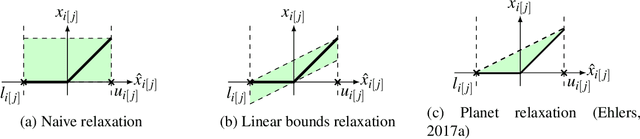
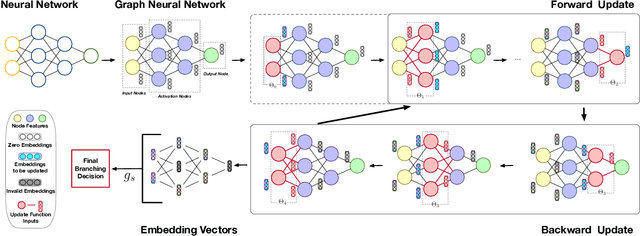
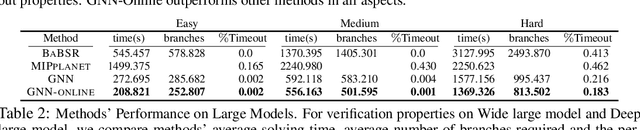
Many available formal verification methods have been shown to be instances of a unified Branch-and-Bound (BaB) formulation. We propose a novel machine learning framework that can be used for designing an effective branching strategy as well as for computing better lower bounds. Specifically, we learn two graph neural networks (GNN) that both directly treat the network we want to verify as a graph input and perform forward-backward passes through the GNN layers. We use one GNN to simulate the strong branching heuristic behaviour and another to compute a feasible dual solution of the convex relaxation, thereby providing a valid lower bound. We provide a new verification dataset that is more challenging than those used in the literature, thereby providing an effective alternative for testing algorithmic improvements for verification. Whilst using just one of the GNNs leads to a reduction in verification time, we get optimal performance when combining the two GNN approaches. Our combined framework achieves a 50\% reduction in both the number of branches and the time required for verification on various convolutional networks when compared to several state-of-the-art verification methods. In addition, we show that our GNN models generalize well to harder properties on larger unseen networks.

Neural Network Branching for Neural Network Verification

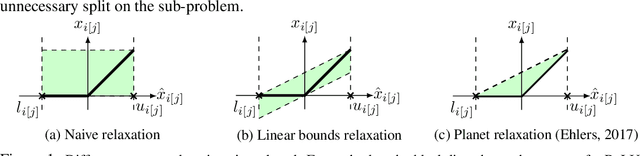
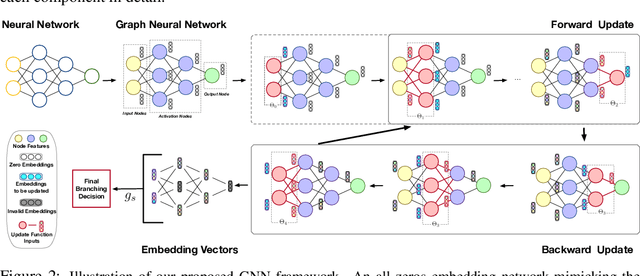
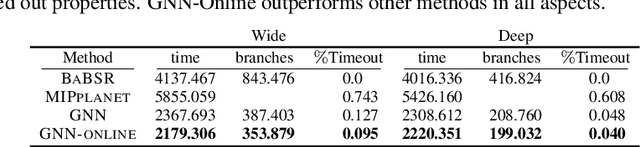
Formal verification of neural networks is essential for their deployment in safety-critical areas. Many available formal verification methods have been shown to be instances of a unified Branch and Bound (BaB) formulation. We propose a novel framework for designing an effective branching strategy for BaB. Specifically, we learn a graph neural network (GNN) to imitate the strong branching heuristic behaviour. Our framework differs from previous methods for learning to branch in two main aspects. Firstly, our framework directly treats the neural network we want to verify as a graph input for the GNN. Secondly, we develop an intuitive forward and backward embedding update schedule. Empirically, our framework achieves roughly $50\%$ reduction in both the number of branches and the time required for verification on various convolutional networks when compared to the best available hand-designed branching strategy. In addition, we show that our GNN model enjoys both horizontal and vertical transferability. Horizontally, the model trained on easy properties performs well on properties of increased difficulty levels. Vertically, the model trained on small neural networks achieves similar performance on large neural networks.

Branch and Bound for Piecewise Linear Neural Network Verification

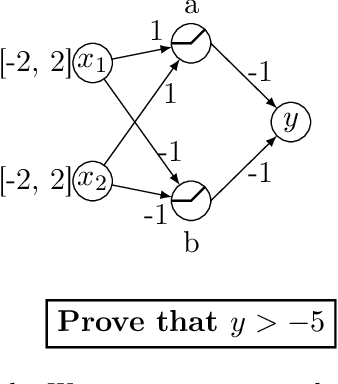
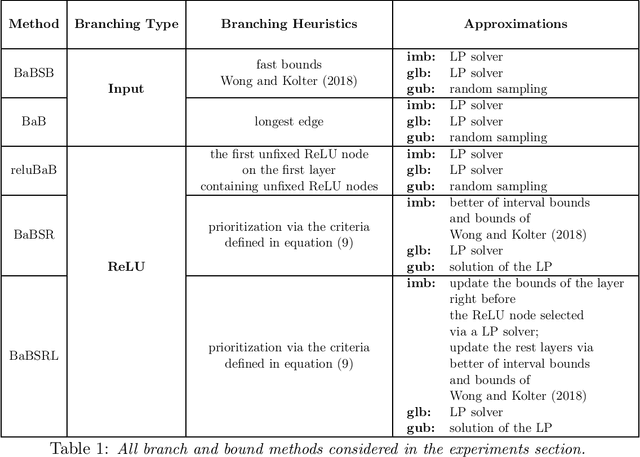
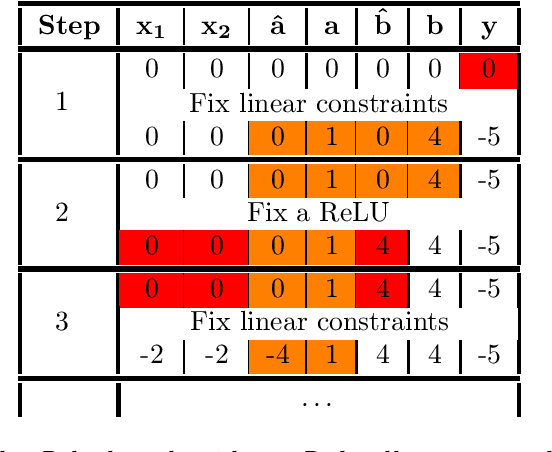
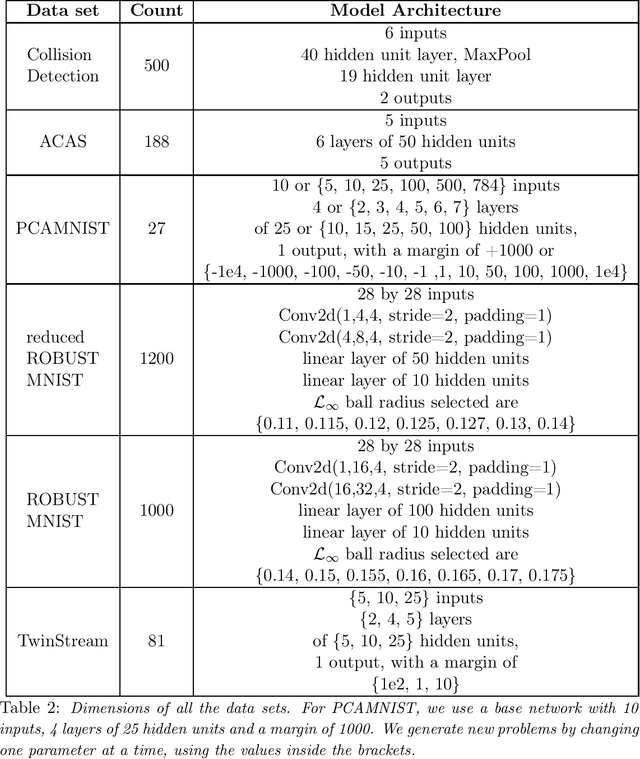
The success of Deep Learning and its potential use in many safety-critical applications has motivated research on formal verification of Neural Network (NN) models. In this context, verification means verifying whether a NN model satisfies certain input-output properties. Despite the reputation of learned NN models as black boxes, and the theoretical hardness of proving useful properties about them, researchers have been successful in verifying some classes of models by exploiting their piecewise linear structure and taking insights from formal methods such as Satisifiability Modulo Theory. However, these methods are still far from scaling to realistic neural networks. To facilitate progress on this crucial area, we make two key contributions. First, we present a unified framework based on branch and bound that encompasses previous methods. This analysis results in the identification of new methods that combine the strengths of multiple existing approaches, accomplishing a speedup of two orders of magnitude compared to the previous state of the art. Second, we propose a new data set of benchmarks which includes a collection of previously released test cases. We use the benchmark to provide a thorough experimental comparison of existing algorithms and identify the factors impacting the hardness of verification problems.